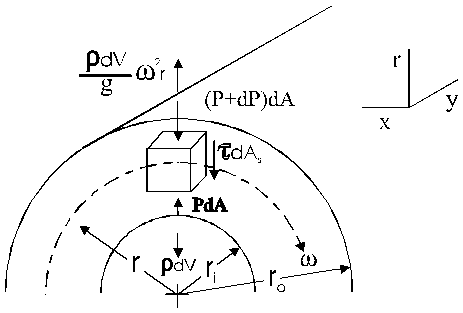
w = angular vel. rdn/sec
P= pressure lb/ft^2
dA = incremental area of end of element ft^2
dAs= incremental area of side of element ft^2
t = shear stress lb/ft^2
As a teacher of materials processing, I have come across various statements in reference material which I incorporate into my course after verifying the information from independent sources..
One topic from this course is the object of this paper. That topic is centrifugal casting. This type of casting uses a long hollow cylindrical tube lined with a suitable ceramic. This tube is so mounted so that it may be spun about its longitudinal axis usually in a horizontal position. The metal to be cast is poured in one end and as the tube spins the molten metal is forced to the inside of the tubes outer surface forming a hollow cylinder. Lengths and wall thickness can vary with tubes up to 30 feet long with 6 inch walls routinely cast.
In preparing lecture material on this subject, statements as to the pressure inside the casting while it is spinning have been found. [1,2] . Since the temperatures inside the casting are those of molten metal, I have wondered how these pressures have been determined. Knowledge of these pressures is necessary for a better understanding of the events that take place within the casting as it spins and cools. Here, I will paraphrase statements made ina a publication on centrifugal casting prepared by the Sandusky Foundry and Machine Co. [3]. As the mold spins, a radial pressure gradient is established across the molten metal, which will become the cylinder wall, the higher pressure being at the surface between the metal and the mold inner surface decreasing to the inner surface of the casting. Directional solidification progresses inward from the mold inner surface. The high radial pressure gradient insures that full feeding of liquid metal is available to offset the solidification shrinkage as the metal cools resulting in very sound metal. This feeding of shrinkage is obtained at pressures which are many times greater than those available by conventional sand casting. To obtain similar pressures in a sand casting would require a sprue height which is impossible to obtain.
Gases liberated during cooling along with dross and other low density materials are forced to the inner surface insuring very sound metal within the interior of the casting wall. These unwanted elements can be machined off during the boring of the inner surface.
It is to be noted that pressures that are too high can result in longitudinal and circumferential cracking as the solidifying metal pulls away from the mold wall. [2]
One additional factor is the design of the mold itself, which requires knowledge of the pressures that act on it for selecting the mold material and thickness. There are other factors influenced by the pressure in the rotating casting which are not addressed here.
This line of inquiry has lead to a mathematical modeling of the process. The following analysis is the result.
Consider an incremental volume dV of a rotating mass of molten metal turning at an angular velocity w about the longitudinal axis y. The forces acting on it are shown in the figure. r is the radius to the center of the volume. The centrifugal force is radially outward, while the inward forces are those due to the pressure differential, gravity, and the shearing force due to the viscosity of the molten. The shearing force is directly a function of the metal viscosity that increases as the molten metal cools. It is included initially for the sake of completeness of the derivation but is neglected in the final integration for the sake of simplicity since this is to be only a first approximation of the pressures.

The sense of the inertia vector is dictated by D’Alemberts principle rendering the summation of the forces in the radial direction zero. It is to be noted that the position of the incremental element is at the top of the rotating cylinder. A different location would result in a different force arrangement but since this analysis is intended to be a first approxmation the location is considered adequate.
The element of liquid considered is the rectangular volume ,dV =drdxdy.
Summing forces if the radial direction yields
S Fr = 0=(r dr dArw ^2 )/g –dPdA -t dAs - r drdA
where dA =dxdy, dV =drdA, dAs = 2(dx + dy) dr
so ( r drdxdyrw ^2)/g –dPdxdy -2t (dx +dy)dr- r drdxdy =0
neglecting t and dividing through by (dxdy)
r rw ^2 dr/g –dP -r dr =0
integrating between r, the distance to any point within the casting, and ri
P = ((r w ^2)/2g) (r^2-ri^2) -r (r –ri)
Doyle in reference 1 states that an aluminum alloy revolved at 2600 rpm experences a pressure of 32 psi at a diameter of 4 inches resulting in a equivalent static head in excess of 26 ft of aluminum. He cites no inner diameter. Using the preceeding equation with the assumption that d=3.75 inches, di =0 (where d is the appropriate diameter) and r = 168.48 lb/ft^3, P turns out to be 32.52 psi and the equivalent head is 27.35 ft of aluminum. Using 4 inches for the outer diameter and 1 inch for the inner diameter results in a pressure of 34.8 psi and the equivalent head of 29.7 ft.
Sandusky Foundry and Machine Co. a specialist in centrifugally cast tubes and cylinders, lists some pressures in a rotating cylinder of stainless steel in their publication "The Manufacture and Properties of Centrifugally Cast Steel Pipe and Other Tubular Products" These data were checked against the above equation at 2 points with the following results:
Molten stainless steel rotated at 500 rpm
point 1: d = 24 inches di = 18 inches
point 2: d = 20 inches di = 18 inches
For point 2 the Sandusky data is 18.9 psi. The equation gives 18.1 psi.
References
[1] Doyle,L.E. et al (1985) Manufacturing Processes and Materials for Engineers 3rd ed. Prentice Hall, Englewood Cliffs, New Jersey
[2] The Manufacture and Properties of Centrifugally Cast Steel Pipe and Other Tubular Products (1959) Sandusky Foundry and Machine Co. Sandusky,Ohio
[3] Centrifugal Casting (no date) Sandusky Foundry and Machine Co., Sandusky, Ohio.