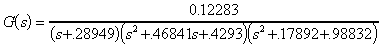
by
Guillermo Rico
gurico@nmsu.edu
Department of Engineering Technology
New Mexico State University
Abstract
Simple procedures for obtaining design formulas for low-pass and high-pass Chebyshev filters are presented. Design is based on the assumption that Chebyshev polynomials are available in mathematical or electrical handbooks. An example describes in detail the design of a specific low-pass filter.
Chebyshev polynomials are found in filter design handbooks. For example, the normalized transfer function (cut-off = 1 rad/sec) for a 1-dB ripple, 5th order low-pass Chebyshev filter is:
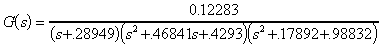
This function can be implemented by cascading two 2nd-order blocks and one 1st- order block. Design steps involve algebraic manipulation and scaling prior to determining resistor and capacitor values.
The op-amp circuits below are low-pass, unity-gain blocks with their corresponding transfer functions.
2nd-order block 1st-order block
The R and C values of each block transfer function must satisfy the
coefficients of the corresponding polynomial properly scaled in
frequency, that is, with s divided by the cut-off frequency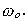
Each block is designed independent of the
others. Let us first look at the low-pass filter design.
In general, we deal with two types of polynomials from
the denominators: first order and second order. Obviously,
even-ordered filters do not include a first-order polynomial and do
not require a first-order block.
Design of a first-order block is straightforward since it only
contains one s-term. First, divide the normalized 1st-order
polynomial of the form (s + alpha) by alpha to obtain the
new polynomial (ßs + 1), where ß=1/a; then replace s by
and equate the term
to sRC to solve for C as follows.
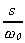
First-order block design
1. Determine ß.
2. Pick a suitable value for R. (5K to 20K is a reasonable
range.)
3. Calculate C using the desired cut-off frequency in rad/sec.
For the 2nd order blocks, we need to equate coefficients for both
s and s 2 terms. The following general steps describe the
process for deriving the design formulas.
a. Divide the normalized 2nd-order polynomial of the form
s 2 + b1s + b0 by b0 to
obtain the new polynomial a2s2 +
a1s + 1. This puts it in the same form as that from the
block transfer function given above.
b. Replace s by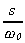
and equate resulting terms to those from the 2nd-order block
transfer function.
c. Solve for C2
d. Solve for C1
Second-order block design
1. Obtain the coefficients a2 and a1.
2. Pick a suitable value for R.
3. Determine C2 using the selected value of R and the
desired cut-off frequency in rad/sec.
4. Calculate C1 using the value of C2 just
found.
As an example, let us design a 5th-order, 1-dB ripple low-pass
filter with a cut-off frequency of 10 Krad/sec or 1.592 KHz using
the 5th-order normalized transfer function shown at the beginning.
First-order section:
Second-order section # 1:
Second-order section # 2:
Verification of the design can be easily done by simulating the filter using any circuit simulation package such as PSpice. When specifying component values, keep four significant digits to maintain accuracy and obtain a tru Chebyshev response. Best results are obtained when op-amps are modeled with ideal or semi-ideal circuits, as opposed to macromodels from commercial op-amps.
HIGH-PASS FILTERS
2nd-order block 1st-order block
To transform a low-pass transfer function to high-pass, it is
necessary to replace s by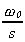
in the
denominator polynomials of the form s + alpha; and s2 + b1s + b0 and rearrange. Equate
similar terms with sRC + 1 and
s2R1R2C2 +
2sR1C + 1 to obtain the following design formulas.
First-order block:
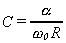
Second-order blocks:
The design sequence can be easily seen to be:
1. Pick R1.
2. Determine C.
3. Calculate R2
Although Chebyshev filters may not be very popular in actual commercial or industrial applications, they are very interesting to work with in the classroom as they represent a very important class of filters. Verification of filter response should probably be limited to simulation on the PC as the filter parameters are quite sensitive to component value deviations necessary for the actual implementation.
Regarding the most popular Butterworth filters, an interesting point regarding their characteristic polynomials, is that they allow the inclusion of 3rd-order blocks that reduce the total number of op-amps required. Reference [3] includes design tables for Butterworth filters.
A relatively simple procedure for obtaining design formulas for Chebyshev filters was presented. The resulting formulas are short and straightforward to use, and yield complete designs in a relatively short time. It is worthwhile to mention that these formulas can be applied to other types of filters such as Thompson, Cauer, and others. As long as the normalized transfer function is known, the design formulas will yield component values that will make every block emulate any specific low-pass or high-pass function.
[1] Stephenson, F.W. (editor), RC Filter Design Handbook, WILEY, 1985.
[2] Van Valkenburg, M.E., Analog Filter Design, HRW, 1982.
[3] Stanley, W.D., Operational Amplifiers with Linear Integrated Circuits, 3rd. edition, MERRILL, 1994.
