Newtons, Slugs and Kilograms Force

from the Technology Interface

by
Ed Gohmann
EGohmann@IUSMail.IUS.Indiana.Edu
Purdue University School of Technology
New Albany, Indiana

The term metric slug appears as a footnote in the 1967 seventh ed of Marks Standard Handbook for Mechanical Engineers. On the same page there is a discussion of kilograms mass and kilograms force. These terms come as a surprise to students who have bee n taught that mass in the metric system was kilograms and force was newtons. They are further awakened when presented with a spring scale calibrated in kilograms, use a Rockwell hardness with loads measured in kilograms or find the term kilogram force in a bearing catalog. Additional concern arises when in a dynamics course they are told to divide the weight of an object by g to obtain its mass in slugs but that the mass in kilograms is not divided by the metric g. Some have difficulty in making the disti nction between the two systems wanting to divided kilograms mass by g. In an effort to clarify the matter the metric slug was revived .

Newton’s second law is written as:

F= ma

with the units for F, m, and a consistent to the system of units being used be it English or metric. Some insight into the units to be used can be obtained by first stating that

Assuming a linear proportion gives

or

Thus for any system of units the value of 1/K must be determined.

In the meter-kilogram mass-second system it is defined that one Newton (N) of force will accelerate 1 kilogram mass (kgm) 1 meter per second squared. Thus for the mkgs system

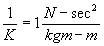
or practically

F (N) = ma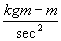

A parallel is found in the English system which defines that 1 pound force (lbf) accelerates 1 slug mass 1 ft/s² resulting in

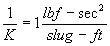
or

F(lbf) = ma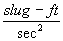

Quite often in this system mass is given in pounds mass (lbm) with the fact that one slug equals 32.17 lbm. Thus to obtain slugs when given lbm you divide by 32.17 lbm/slug.

F(lbf) = ma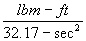

OR

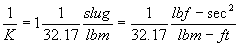
To determine the mass of an object a beam balance could be used giving either lbm or kgm. To determine weight, a spring scale calibrated in either Newtons or lbf would be used. However spring scales are available which measu re weight in kilograms which are actually kilograms force.

Kilograms force bears the same relationship to kilograms mass that the pound force bears to the pound mass.

That is

F(kgf)= 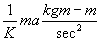(1)

Here

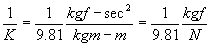
Now

= 9.81 N (2)

which is the weight of 1 kgm when g=9.81 m/s².

Also from eq (1)

W=( 1 kgm x 9.81 m/s²) / (9.81 kgm-m /kgf-s²) = 1 kgf (3)

which is the weight of one kgm when force is measured in kgf.

It follows then that 9.81 N = 1 kgf from eq (2) and (3).

Returning to Newton’s second law, if , analogous to lbf and slugs, a kgf is said to accelerate an unspecified mass 1 m/s² then that mass is equal to the metric slug.

For example a 10 kgm mass accelerated at 3 m/s² requires a force of 30 N. If ,on the other hand, the weight is given as 10 kgf instead then

F = ( 10 kgf/9.81) x 3 m/s²

=3.058 kgf

since 1 kgf =9.81 N

Students are usually told that near the earth’s surface, the magnitude of lbm = the magnitude of lbf and the magnitude of kgm = the magnitude of kgf.

These are no longer true when the acceleration of gravity is non-standard.

It is hoped this exercise will impress further upon the student the care that must be taken when dealing with the US customary units and the SI units.

1. Shames,I.H. (1997 ). Engineering Mechanics: Statics) ( 4th ed. ). New Jersey: Prentice Hall.

2. Holman, J.P. ( 1963 ) Heat Transfer . New York: McGraw-Hill

3. Baumeister,T. (ed) and Marks, L.S. (ed 1916-1951). (1967).

Standard Handbook for Mechanical Engineers ( 7ed ). New York: McGraw-Hill