Statistical Techniques Useful

for the Foundry Industry

by

Matthew E. Elam	Robert G. Batson
Matthew_Elam@tamu-commerce.edu	rbatson@eng.ua.edu
Dept. of Industrial Engineering and Technology Texas A&M University-Commerce	Industrial Engineering Program University of Alabama-Tuscaloosa

 

 

Abstract: The foundry industry produces cast metal products for consumers, public works, and other industries such as automotive.  It constantly struggles with casting problems resulting from material and processing conditions.  This paper considers several of these problems in its documentation of two foundry industry projects.  One project studies cast weight variability and the other evaluates pin hole problems with castings.  Each project's solution methodology is presented in detail along with the statistical techniques used.  By following these methodologies, foundries will be able to analyze problems identical to those addressed by the projects.  Foundries may also recognize other problems the statistical techniques may be helpful in analyzing.

I. Introduction

The foundry industry produces cast metal products for consumers, public works, and other industries such as automotive.  A variety of metals are cast and numerous casting methods are used, including centrifugal (for pipes), sand mold, lost foam, and static (for large objects).  Castings are subject to surface and internal defects resulting from material and processing conditions.  Particular combinations of these conditions cause defects and other variation in products.  The foundry industry also encounters problems with quality common to most other types of industries, such as not meeting specifications and excess variability in measurement systems.

 

This paper considers several of these problems in its documentation of two foundry industry projects.  One project studies cast weight variability and the other evaluates pin hole problems with castings.  Cast weight variability refers to variation, or unevenness, in pipe wall thickness.  If the pipe wall is too thin in some areas, foundries may have to downgrade or scrap the pipe.  To prevent this, foundries may put more raw material into the pipe wall to make it thicker in the thin areas.  However, giving away raw material in this manner can be costly.  The only way to prevent these scenarios is to reduce the cast weight variability.  Pin holes are cavities in thick sections of machined surfaces or a series of fine holes on machined skin.  They can cause castings to "weep" under pressure tests.  Pin holes are caused by the presence of hydrogen gas, nitrogen gas, or manganese oxide in the metal [1].

This paper presents each project's solution methodology in detail along with the statistical techniques used.  By following these methodologies, foundries will be able to analyze problems identical to those addressed by the projects.  Foundries may also recognize other problems the statistical techniques may be helpful in analyzing.

II. Cast Weight Analysis

This project was at a foundry that weighed each produced pipe twice.  The first, or cast, weight was obtained using scales in the pipe shop immediately after extraction from the machine.  The second, or shed, weight was obtained using scales in the inspection shed two to four hours after production.  The shed weight was considered official.  Pipe that was too light for its class was downgraded to a lower class.  While downgrading helped with the cost of underweight pipe, it was undesirable.  Underweight pipe meant it weighed less than the minimum weight for its diameter and class.  Minimum weight was always 95% of standard weight (as defined by the American Water Works Association (AWWA)).

 

The variation in the cast weight of pipe was an ongoing concern for this foundry.  This variation was investigated using tools such as gauge repeatability and reproducibility (R&R), comparative studies of the two scales on the same pipes, control charts, correlation, and regression analysis.  The objective of these various approaches was to identify the extent of the variation, statistically significant causes of the variation, and potential action available to the foundry to reduce the variation.  This would help the foundry save money by using less molten iron to achieve the same pipe production.

 

2.1 Database

 

The database provided by the foundry was an Excel [2] file with each row representing one pipe.  Many columns of materials and processing variables were provided in the spreadsheet for each row of pipe, including cast, shed, standard, and minimum weights.  The data were organized in order of production in the shop.  Several machines were used in the multi-day run reported in the spreadsheet.  There were two diameters of pipe in the database.  The joint type was fixed during the entire run.  Ten data sets were identified with which to perform analyses by stratifying the database according to the variables provided.  Stratification involved grouping rows of data in the database by variables that have very different effects on the different groups.  The groups were then analyzed separately.

 

2.2 Preliminary Analysis

 

Individuals and moving range control charts were applied to cast weights, cast weight deviation from standard weight, and cast weight deviation from minimal weight to establish statistical control of the data.  Patterns on the charts were interpreted both before and after the deletion of points.  Additionally, coefficient of variation calculations were performed and histograms were constructed both before and after the deletion of points.  All of these analyses were performed in the Minitab [3] statistical software package.

The histograms revealed that the average cast weight was much too high.  The relationship between the left, or lower, end of the histograms and the appropriate minimum weight indicated that adjustments could be made to the process to run at the lower standard cast weight.  This would give away less material without increasing underweight pipe.

 

Similar statistical analyses were performed in Minitab [3] for the shed weights.  It was concluded that the standard deviation calculations within each of the ten data sets were similar to those for the cast weights.  However, the average calculations within each of the ten data sets were quite different than those for the cast weights.  This led to the conclusion that the machine and shed scales were not aligned.  It was important for the shed and cast weights to be aligned, or for there to be a known difference in the two measurements.  This allowed for the target cast weight to be adjusted up or down to make the shed weights come out in a probability distribution whose low end tail stops at approximately the minimum weight, with adequate allowance for the imprecision of the measurement system itself.  If the shed and machine weights were kept aligned by more frequent adjustments, then compensatory movement of the target would be eliminated.  This would make the target casting value easier to specify (it would be a function of the process and measurement system standard deviations for the specific pipe size and class being run).

 

2.3 A Method to Determine Target Weights for Casting

 

A gauge R & R (repeatability and reproducibility) experiment was performed on the scales located at two different casting machines.  It involved weighing the same pipe twice.  The values obtained for measurement precision were needed to set the target cast weight for each pipe size and machine.  Equation (1) was developed by the authors for determining the target weight for producing any size and class of pipe in the database on any one of these two casting machines:

 

(1) TA = MW + 3.5 × SD + 3.0 × PR

 

The variable TA is the target, MW is the minimum weight, SD is the in-control standard deviation of the process, and PR is the precision of the machine scales.  The 3.5 factor assured that running at the target would produce no more than 23 out of 100,000 underweight pipe.  If a factor of 3.0 had been used instead, then the assurance was no more than 135 out of 100,000 pipe would be underweight.  These factor values were evaluated by testing Equation (1) with the Excel [2] database provided by the foundry.  The origin of Equation (1) was the third-to-last and last sentences of Section 2.2.

 

2.4 Correlation Analysis of Materials and Process Variables with Cast Weight

 

Focusing on a specific run in the database, scatter diagrams of cast weight vs. each process variable in the columns of the database were studied.  The scatter diagrams were constructed using Minitab [3].  Minitab [3] was then used to compute Pearson correlation coefficients r (-1 < r < 1) for cast weight vs. each process variable.  An r of -1 indicated a perfect negative linear relationship, meaning that as one variable increased (decreased), the other variable decreased (increased).  An r of one indicated a perfect positive linear relationship, meaning that as one variable increased (decreased), the other variable also increased (decreased).  An r equal to zero indicated no linear relationship existed; however, this did not mean there was no relationship between the two variables under consideration.  For example, there could be a quadratic relationship between the two variables.  Scatter diagrams revealed these types of relationships.

 

The results of this analysis are in Table 1, which shows the ten variables (coded to protect the anonymity of the foundry) that had a statistically significant sample correlation coefficient r with cast weight.  This statistically significant relationship was indicated by the p-values (0 < p-value < 1) for each value of r.  P-values close to zero (less than 0.100) indicated a statistically significant result.  The fact that these ten correlation coefficients had absolute values ranging from 0.276 to 0.535 was not discouraging.  In complex manufacturing processes, such weak-to-moderate correlations can be useful for control when true casual relationships are proven to exist.  Input from the foundry's experts was necessary to determine if the statistically significant correlations implied a cause and effect relationship.

 

The signs on the correlation coefficients in Table 1 were also important.  These indicated if cast weight increased (+) or decreased (-) as the process variable increased.  The scatter diagrams mentioned earlier all presented patterns that supported the signs and magnitudes on these ten correlation coefficients.  Finally, these same scatter diagrams were studied to determine if any of the ten variables exerted some control on the standard deviation of cast weight.  As shown in the final column of Table 1, four of the ten variables were identified as potentially controlling the standard deviation of pipe cast weight.

 

2.5 Regression Model-building for Cast Weights

 

The final step in the analysis was to attempt to build first order polynomials relating cast weight (the response) to pairs of the controlling variables.  These regression studies revealed which pair of control variables best predicted the cast weight.  They also revealed any interaction between pairs of control variables.  Using the ten process variables identified in Table 1 as linearly correlated with pipe cast weight, a multiple regression study was conducted in Minitab [3].

 

All possible linear models of cast weight versus pairs of the ten variables were fit, including the interaction term for the respective variables.  From among those, twelve had acceptable regression diagnostics such as R² (the coefficient of determination), significance of regression F-

 

 

 

 

 

 

 

 

 

Table 1: Pipe shop process variables correlated with cast weight

 

test, significance of coefficient t-tests, and residual plots.  These 12 models are summarized in Table 2.  Seven of the models had a significant interaction between the two independent variables relative to the cast weight of pipe produced under those conditions.  One model (#4) rejected the interaction because it was insignificant.  Model #4 also rejected the paired variable because it was correlated with the first variable, resulting in a single variable model.

 

The sign, magnitude, and pattern of the significant variables in the models were also studied to determine if there was an opportunity to establish control rules.  The following was concluded:

• Looking down the columns of Table 2, there are inconsistent signs on the coefficients for a given independent variable across the models.  This means that there is no guidance in the models on whether increasing the independent variable would cause the cast weight to increase or decrease.
• The variable F appeared in seven of the 12 models, twice as often as any other variable.  This was one indication that the variable F required more investigation as to how it might

 

Table 2: Summary of the twelve regression models

 

 

affect cast weight.  The variable F also had the largest magnitude correlation coefficient among the ten variables (see Table 1).

• Variables F and H had the largest magnitude coefficients in the models, hence the largest magnitude potential impact on cast weight if they vary from pipe to pipe.  It was recommended that the foundry determine how these variables may affect cast weights.

III. Pin Hole Analysis

The second foundry project was to determine relationships (if any) between casting machine parameters and pin holes in pipe.

 

3.1 Database Used for the Analysis

 

The existing Excel [2] database of casting machine parameters provided by the foundry was insufficient because it did not include a response that represented the pin hole problem.  The foundry agreed to examine a smaller sample of pipes and record pin hole counts for them in addition to the usual casting machine parameters.  Fifteen pipe numbers were randomly generated for each of three days production in the pipe shop.  A list of the 15 random pipes to be held for examination was issued each day.  Thirty-seven (11 the first day and 13 the next two days) of the 45 total pipes listed for examination were actually held due to administrative and logistical barriers.  The pipes tested were of various diameters and classes.  To determine pin hole counts, a 4.0"´4.0" cutout was overlaid on the worst pin hole area on a pipe and the number of pin holes within this cutout was counted and recorded.  The foundry developed this procedure because it did not have an automated system for counting pin holes.  Manually counting pin holes was very time consuming and error-prone.  This was due to the large diameters and long lengths of the pipes produced by the foundry.  The worst pin hole area in this procedure was judged to be the one with the most pin holes that had the deepest penetration into the pipe wall.  The foundry had guidelines for determining the depths of pin holes that caused pipe to be scrapped.  Of course, pin holes that traveled from the exterior to the interior wall of the pipe caused the pipe to be scrapped.

 

3.2 Plan to Reduce Pin Holes

 

The following plan was undertaken to reduce the number of pin holes in pipes:

Step 1. Investigate the variables in the new database vs. the number of pin-holes and choose those variables that are related to the number of pin-holes for further analysis in step 2

Step 2. Investigate the variables remaining after step 1 vs. each other (those variables that are related to each other will require the input of process experts about which variables are the cause of the relationship)

Step 3. Determine the levels of the variables remaining after step 2 that minimize the number of pin-holes and monitor them at those levels using control charting techniques

 

 

 

3.3 Pre-Analysis

 

Prior to the investigation, the new database was examined to determine what (if any) stratification should be performed and which of the 75 casting machine parameters should be included in the analysis.  The first stratification performed was by each of the three different days the pipe data were collected.  The second stratification performed was by pipe diameter within the first stratification.  This was done because of the different values of many of the casting machine parameters in the new database for different pipe diameters.  It would have been desirable to stratify by additional casting machine parameters.  However, because of the limited amount of data available for the analysis, it was not done.

 

The guideline used in determining which casting machine parameters should be included in the analysis was how many different values each casting machine parameter had for each of the different groupings of the data after stratification.  Several different values were needed for each grouping to get an idea of the relationship (linear or otherwise) of the parameters with the response (pin holes).  Many of the 75 casting machine parameters were eliminated from the analysis for this reason.

 

3.4 Revised Database

 

Stratification and parameter selection resulted in a revised database with 15 casting machine parameters along with the number of pin holes.  As stated previously, the pipes selected for analysis were determined using randomly generated pipe identification numbers.  Because of this randomness, only one pipe diameter had enough rows of data (seven) to be evaluated for the first day.  For the second day, only one pipe diameter different from day one had enough rows of data (ten) to be evaluated.  For the third day, only one pipe diameter different from days one and two had enough rows of data (eight) to be evaluated.  These sample sizes can be considered small by statistical standards, but it is very time consuming to manually count pin holes on pipes.  It was suggested that the foundry investigate automated approaches to count pin holes.  If an approach could be found or developed, then pin hole counts could be added to the database of parameters measured for each pipe.

 

3.5 Analysis

 

Investigations were performed using scatter plots and Pearson correlation analysis in Minitab [3].  The three steps below describe what was done and what was concluded for each of the three steps in subsection 3.2.

 

Step 1

Scatter plots were constructed and correlations were calculated for the number of pin holes vs. each of the 15 casting machine parameters for each of the three days.  For example, the scatter plot for the number of pin holes vs. casting machine parameter #24 (coded to protect the anonymity of the foundry) is Figure 1.  The correlation results also provide p-values.  Table 3 shows the resulting Pearson correlation values and their corresponding p-values (in parentheses) for the five casting machine parameters that had a statistically significant relationship with the number of pin holes.  The Pearson correlation value with a single asterisk "*" was not

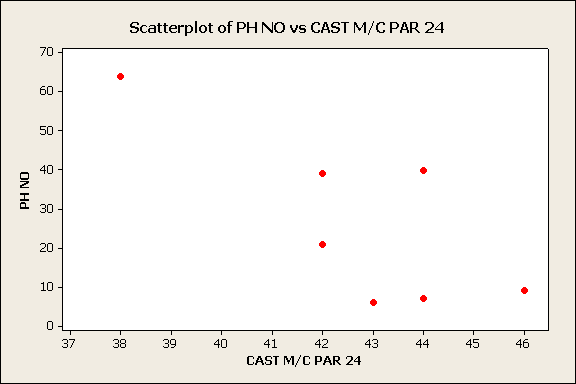
Figure 1: Scatter plot for the number of pin holes (PH NO) vs. casting machine parameter #24 (CAST M/C PAR 24)

 

 

Table 3: Pearson correlation values and corresponding p-values

(in parentheses) for casting machine parameters vs. number of pin holes

 

 

representative of a statistically significant relationship, but the respective scatter plot indicated a potential quadratic relationship.  Only casting machine parameter #32 appeared on more than one day.  These relationships can be used in step 3 to determine control procedures for alleviating the pin hole problem.

 

Step 2

The following comparisons between the five casting machine parameters from Step 1 were performed:

• For Day 1, casting machine parameters #24, #28, and #32
• For Day 2, casting machine parameters #14 and #15

 

Scatter plots and correlation results indicated the following relationships:

• For Day 1, casting machine parameters #24 and #28 had a linear relationship (the Pearson correlation value was -0.826 with a p-value of 0.022)
• For Day 1, casting machine parameters #24 and #32 appeared to have a quadratic relationship
• For Day 2, casting machine parameters #14 and #15 had a linear relationship (the Pearson correlation value was 0.797 with a p-value of 0.006)

 

The input of the foundry's process experts was necessary to determine if any of these relationships were practical and, if so, what casting machine parameter or parameters were causing the relationship.

 

An additional issue was whether or not any of the five casting machine parameters in Table 3 interacted with each other in a statistically significant way.  This could have been checked by building regression models with an interaction term for each day.  However, because of the relationships between the five casting machine parameters, this was not done due to multicollinearity issues that would arise with the resulting regression models.  Multicollinearity is the term used to describe the occurrence of correlation between independent variables.

 

Step 3

The following conclusions were drawn regarding the levels of the casting machine parameters and their effects upon minimizing the pin hole problem after the initial data analysis and prior to discussions with the foundry's personnel:

• If casting machine parameter #14 is chosen to be monitored, it should be kept as low as possible (relative to what the foundry has experienced with certain pipe diameters) to prevent pin holes from going up
• If casting machine parameter #15 is chosen to be monitored, it should be kept as low as possible (relative to what the foundry has experienced with certain pipe diameters) to prevent pin holes from going up
• If casting machine parameter #24 is chosen to be monitored, it should be kept at higher levels (relative to what the foundry has experienced with certain pipe diameters) to prevent pin holes from going up
• If casting machine parameter #28 is chosen to be monitored, it should be kept as low as possible (relative to what the foundry has experienced with certain pipe diameters) to prevent pin holes from going up

IV. Conclusions

It was suggested to the foundries that the findings and recommendations of the projects initially be put into action on a very small scale.  Once positive results were achieved, then incremental steps could be taken over an extended period of time to more fully implement them.  Also, the foundries were informed that the findings and recommendations of the projects may not be true after an extended period of time due to process changes, both intentional and natural, that may occur.  However, the procedures used in the projects may be followed to analyze new data when changes are suspected.  Finally, the foundries were advised that the findings and recommendations of the projects should be taken within the context of the databases made available.

 

The statistical techniques used in this paper have been successfully applied to problems other than cast weight and pin hole issues.  For example, correlation analysis was performed to determine if a relationship could be established between the composition of castings (i.e., the concentration of carbon (C), silicon (Si), etc.) and the required critical properties of the castings [4].  Also, regression analysis was used to investigate relationships between the properties (yield, tensile, and elongation) of steel tubes after cold working and those of flat coils before cold working [5].

 

Many statistical techniques not covered in this paper can also be used by the foundry industry.  For example, Taguchi techniques have been applied to determine parameters and their optimal settings for improving the quality of castings produced by a V-process, a sand molding process [6].  Also, response surface methodology (RSM) was used to determine the influence of different parameters on the mechanical properties of Aluminum (Al)-Silicon (Si) alloy castings [7].

 

 

 

 

 

References

[1]    Datta, G.L. "Casting Defects – Causes and Remedies," Indian Foundry Journal, 42(1), 14-21, 1996.

 

[2]    Excel. Microsoft Office Professional Edition, Microsoft Corporation, 2003.

 

[3]    Minitab. Release 14.1, Minitab Inc., 2003.

 

[4]    Kippola, D.E. and Goodrich, G.M. "Factors Affecting Ductile Iron’s Impact, Tensile Strength," Modern Casting, 91(4), 42-44, 2001.

 

[5]    Zhang, J. Statistical Analysis of Cold Working Effect on Steel Tube Manufacturing, M.S. Non-Thesis Research Report, Department of Industrial Engineering, The University of Alabama, Tuscaloosa, AL, 2002.

 

[6]    Kumar, P., Barua, P.B., and Gaindhar, J.L. "Quality Optimization (Multi-Characteristics) through Taguchi's Technique and Utility Concept," Quality and Reliability Engineering International, 16, 475-485, 2000.

 

[7]    Kumar, S., Creese, R.C., Kumar, P., and Shan, H.S. "Investigation of the Effect of Process Parameters on the Mechanical Properties (Tensile) of Al-7%Si Alloy Castings Produced by Evaporative Pattern Casting Process," Indian Foundry Journal, 50(7), 21-29, 2004.