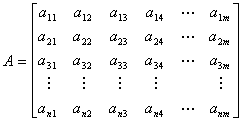
the Technology Interface / Fall97

A computer program, written in the C language, has been developed to aid students who are learning to solve electric circuit problems involving the mesh analysis and nodal analysis techniques. The program solves the system of equations generated when using the above techniques for the case of complex variables. The software is user-friendly and may be freely copied for educational use. In this paper, an overview of circuit analysis is presented, followed by a description of the software and the solution of a sample circuit, including a run-time listing of the program.

In the study of electric circuits, the typical task is to determine the current(s) and voltage(s) in a circuit. In order to determine the voltages and currents (a process that is sometimes referred to as "solving" the circuit), a number of standard techniques is available. For relatively simple circuits containing only one independent source (or multiple sources that can be combined into one), series-parallel analysis techniques are sufficient. However, for complex networks, more sophisticated analysis techniques can be utilized. Two such techniques are mesh analysis and nodal analysis.

The mesh analysis technique involves determining the minimum set of circuit loops, and applying Kirchhoff's Voltage Law (KVL) to each of them. This process results in a system of linear equations in which the loop currents are represented by the variables, the impedances are represented by the coefficients, and the circuit sources appear as constant terms. Similarly, the nodal analysis technique involves determining the minimum set of circuit nodes, and applying Kirchhoff's Current Law (KCL) to each of them. This results in a system of linear equations in which the node voltages are represented by the variables, the admittances (reciprocals of impedances) are represented by the coefficients, and the circuit sources appear as constant terms [1]. With either technique, the result is a system of n linear equations in n variables. The system can be solved using any number of techniques, such as substitution, Cramer's method, or Gaussian elimination, among others. The number of equations to be solved may suggest a particular method to use. The solution, of course, yields the circuit currents or voltages, from which other circuit quantities can be calculated easily.

For students, problems often occur in solving the equations, due to the large number of algebraic manipulations and arithmetic steps required. This is true especially in the case of alternating current (AC) circuits, because the coefficients and constant terms in the system of equations consist of complex numbers. Thus, the process also involves the conversion of quantities between polar and rectangular forms. Typically, students solve these circuits and then, when their answers do not agree with the correct solution (usually giving by the textbook author), problems arise.

For many years, computers have been called upon to help in solving these circuits. Commercially-available software packages, such as PSpice, are available for modelling and simulating electrical and electronic circuits. While these software packages are useful for students in a variety of contexts, they do too much of the work for the student who is in the process of learning circuit analysis techniques. When a student finds that his paper-and-pencil solution to a mesh or nodal analysis problem does not match the solution obtained by a program such as PSpice, he does not have much information about where he made a mistake. The student does not know whether he set up the system of equations incorrectly, or set up the equations correctly and made errors in solving the system. This can result in much time being spent re-working equations that are not set up correctly in the first place, or in looking for mistakes in solving a system, when no mistakes were made. Because programs such as PSpice go through the entire process of solving the circuit, all in one step, the student has difficulty determining where he went wrong.

As a result, a more useful software tool to use while studying these analysis techniques is one which merely solves the system of equations. This approach allows the student to quickly determine whether he made errors in setting up the system of equations or in solving the system. In other words, the student can compare his hand-written solution with the one generated by the computer, and easily determine whether he solved the equations correctly. Commercially-developed software packages, such as Mathematica and MathCAD, can be used to solve systems of equations for these applications. However, because these software packages are copyrighted, they may not be readily accessible to all students in a class. Furthermore, these software packages are sometimes time-consuming to learn how to use, especially when dealing with complex numbers and matrices.

Thus, the work described here presents a software tool which performs the task of solving systems of linear equations. It is designed to aid students who are learning how to solve circuits using the mesh and nodal analysis techniques. The program is easy to use, because it performs only one function -- solving systems of equations. In addition, the program may be freely copied for educational use, so it can be made accessible to every student in a class.

The program that was developed has been titled SOLE-SOLVER, indicating that it solves Systems Of Linear Equations. The program was written in the C language, and works as follows: The user is requested to input the number of equations to be solved, as well as the (complex) coefficients and constant terms corresponding to the system of linear equations. Then, the program solves the system of equations and the solution is output in both rectangular and polar form.

A brief description of the main program, in pseudocode form, is given below.

• display program information
• display instructions
• get input data
• display the system of equations
• reduce the system of equations
• display the solution
  

The algorithm used to reduce the system of equations is based on the Gauss-Jordan elimination technique. The technique assumes that a system of n linear equations exists in the form of an augmented matrix, consisting of n rows and m columns (where m = n+1). For example, consider matrix A, the n x m matrix shown below.

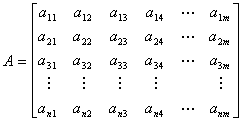
In the matrix, each element, a_ij, is subscripted with a row number i and a column number j, to indicate its position in the matrix. Using this representation of a system of linear equations, the matrix elements in columns 1 to m-1 represent the coefficient terms, and the elements in column m represent the constant terms of the system.

The Gauss-Jordan elimination technique consists of two major parts, as described below. For simplicity, in the discussion that follows, assume that a system of 4 equations is to be solved, and is initially represented by matrix B, the 4 x 5 matrix shown below.

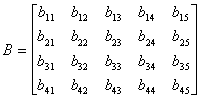
The first part of the elimination technique is to reduce the matrix to "row-echelon" form, in which all of the diagonal elements are equal to 1, and all of the elements below the diagonal elements are equal to 0. This reduction is accomplished using a sequence of row operations on each of rows 1 to 4. Beginning with row 1, the first step is to divide each element b_1j by the value of the row's diagonal element b₁₁, which forces the diagonal element to become equal to 1. Next, in row 2, each element b_2j is multiplied by the negative of the corresponding element b_1j in row 1, and the product is then added to the original value of element b_2j, thus replacing it. This operation forces the value of element b₂₁ to become equal to 0, thus, eliminating the corresponding variable (in column 1) from row 2. The process is repeated to eliminate the same variable from rows 3 and 4. At this point, the entire process just described for row 1 is repeated for rows 2, 3, and 4, which results in a matrix reduced to row-echelon form, as shown below in matrix C.

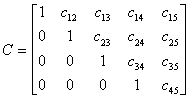
The second part of the elimination technique is to perform a series of row operations on the matrix to convert it from "row-echelon form" to "reduced row-echelon form", in which all of the diagonal elements are equal to 1 and all other elements (except the constant terms in column m) are equal to 0. This is achieved by processing each row, in much the same way as described above, except working from the bottom of the matrix to the top. When completed, the resulting matrix is in reduced row-echelon form, as shown below in matrix D.

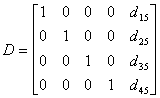
At this point, the elimination process is complete, and there is only one non-zero coefficient term represented in each row of the matrix. As a result, the solution to the system of equations appears in the right-most column of the matrix (column 5). Because performing these row operations on the matrix does not change the system of equations that it represents, the reduced matrix D is equivalent to matrix C, and to the original matrix B. Thus, the solution to the system of equations represented by matrix D is also the solution to the original system represented by matrix B. For further details regarding the Gauss-Jordan elimination technique, the reader is referred to the references [2,3].

To handle the complex numbers required by the program, an abstract data type (ADT) called Complex was developed. This ADT includes operations to make a complex number, to return the real and imaginary parts of a complex number, to return the magnitude and angle associated with a complex number, and operations to perform addition, subtraction, multiplication, and division of complex numbers. These routines were implemented by the author, because they were not available in the library of functions that came with the compiler. A detailed description of ADTs may be found in the references [4,5].

The SOLE-SOLVER program consists of three files: solesolv.c, which contains the main program; solecplx.c, which contains the Complex ADT functions; and solecplx.h, which contains the Complex ADT header information. The SOLE-SOLVER program was compiled using the Borland Turbo C 3.0 compiler, using the following command: tcc -esolesolv.exe solesolv.c solecplx.c [6]. (The program also can be similarly compiled on a Unix system using the Gnu C Compiler, using the command: gcc-o solesolv.exe solesolv.c solecplx.c -lm .) The program was tested by executing it, in a DOS window, on a Pentium-based personal computer (PC) running the Windows 95 operating system. The executable file (compiled for PCs) along with the complete source code listing of the program may be obtained by sending an e-mail request to the author.

To demonstrate the use of the program, consider the use of mesh analysis in solving the following AC network.

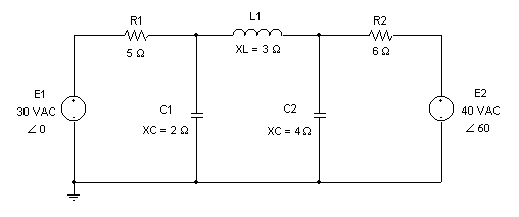
By applying KVL to the three-loop circuit, the following system of equations can be obtained:

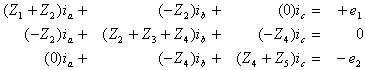
In this system, the impedance values Z₁, Z₂, Z₃, Z₄, and Z₅ refer to the impedances of elements R1, C1, L1, C2, and R2, respectively. After substituting the values for the impedances and the voltage sources indicated in the figure, the system becomes as follows:

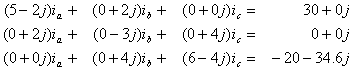
By running the SOLE-SOLVER program, and entering this system of equations into it, the following output is produced:

SOLE-SOLVER v1.1 A program that solves systems of linear equations containing complex elements. (C) 1997 C.L. Robinson This program may be freely copied and used for non-commercial, educational use only. Please report bugs to crobinso@kent.edu This program can be used to solve a system of simultaneous linear equations whose coefficients and constant terms are complex numbers. The program assumes that the number of equations equals the number of variables, and that the system has a unique solution. The input data may be supplied via the keyboard. For convenience, the input data may be stored in a text file and redirected to the program upon execution, using operating system redirection '<'. Please enter the number of equations to be solved: 3 Enter the coefficients and constants for equation 1, in rectangular form: 5 -2 0 2 0 0 30 0 Enter the coefficients and constants for equation 2, in rectangular form: 0 2 0 -3 0 4 0 0 Enter the coefficients and constants for equation 3, in rectangular form: 0 0 0 4 6 -4 -20 -34.64 For this system of equations: (+5.00E+00 -2.00E+00j)x + (+0.00E+00 +2.00E+00j)y + (+0.00E+00 +0.00E+00j)z = (+3.00E+01 +0.00E+00j) (+0.00E+00 +2.00E+00j)x + (+0.00E+00 -3.00E+00j)y + (+0.00E+00 +4.00E+00j)z = (+0.00E+00 +0.00E+00j) (+0.00E+00 +0.00E+00j)x + (+0.00E+00 +4.00E+00j)y + (+6.00E+00 -4.00E+00j)z = (-2.00E+01 -3.46E+01j) The solution to the system of equations is: Rectangular Form Polar Form x = +2.47E+00 + 2.28E+00j x = +3.36E+00 |_ +4.28E+01 y = -3.24E+00 - 6.55E+00j y = +7.31E+00 |_ -1.16E+02 z = -3.66E+00 - 6.06E+00j z = +7.08E+00 |_ -1.21E+02

Thus, the solution to the system of equations is obtained, in both rectangular and polar form. Notice that the values are shown with a maximum of three significant digits, which provides a reasonable level of precision. If desired, the number of digits displayed can be increased by modifying the source code. When compiled on a PC as described, the real and imaginary parts of all complex variables are stored in double-precision floating point format (64 bits), which is sufficient to avoid problems with rounding error, for most exercises that students will encounter in studying circuit analysis. For a detailed discussion of dealing with excessive rounding error in this type of program, the reader is referred to the references [2,3].

The program was designed to solve complex systems of equations resulting from the analysis of AC circuits, meaning those that consist of complex numbers in their coefficient and constant terms. However, the program also can be used to solve systems of equations that represent DC circuits, simply by inputting 0 for the imaginary part of each coefficient and constant term.

For problems involving only two or three equations, data entry via the keyboard is probably the most efficient way to supply the input. However, for larger systems of equations, it is convenient to store the input data in a text file, and then supply it to the program using operating system re-direction. For example, if the input data for a system were placed in a file named circuit1.txt, and the executable file for the program were titled solesolv.exe, the operating system command solesolv.exe < circuit1.txt could be used to execute the program, while taking the input data from the text file. Similarly, the output of the program also could be stored in a text file, using a command such as solesolv.exe < circuit1.txt > output1.txt. The program was designed to accommodate a system of up to 9 equations, which should be sufficient for most problems. To solve a system of more than 9 equations, the only change required in the program is to increase the value of the defined constant MAX_EQU, in the source code.

A computer program was presented for the purpose of helping students in introductory AC circuit analysis courses learn to solve problems involving mesh analysis and nodal analysis. The ease of use and free nature of the program make it a useful, accessible tool for students in associate- and baccalaureate-level technology programs. In fact, the program could be used to solve systems of equations for applications extending beyond circuit analysis, to any problems in which systems of equations need to be solved easily. Because the program was written in the C language, for which compilers are available for many platforms, it can be compiled for either a PC or Unix environment, both of which are common to university computer laboratories.

The source code of the program may be copied and used for educational, non-commercial purposes. The source code may be modified if desired, to suit the user. One possible modification would be to adapt the program to solve systems of equations involving scalar (rather than complex) quantities, for applications such as DC circuits. A further enhancement would be to allow the user to select whether the system to be solved consists of scalar or complex quantities. These modifications, or the development of the entire program, could be an interesting assignment or project for students in computer engineering technology programs.

[1] Boylestad R L, Introductory Circuit Analysis, 8^th ed., Prentice-Hall: 1997.

[2] Larson R E and Edwards B H, Elementary Linear Algebra, Heath: 1991.

[3] Hubin W N, BASIC Programming for Scientists and Engineers, Prentice-Hall: 1978.

[4] Tanenbaum A M, Langsam Y, and Augenstein M J, Data Structures Using C,

Prentice-Hall: 1990.

[5] Deitel H M and Deitel P J, C How to Program, 2^nd ed., Prentice-Hall: 1994.

[6] Borland International, Scotts Valley, California, 95066.